blog

今日の遣り方でも活躍するであろう『カネピタ』について書きたいと思います。

こんな工具です。

写真のように先端のリング2つを引き出すと、2枚の金属テープが同じ長さ出てくるようになっています。
マキガネとも言うそうです。
遣り方の際に、矩(カネ)を出すのに使います。
使用方法は、以下の通りです。
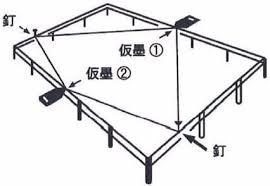
①対向する遣り方貫の基準位置に釘を2本打ちます。

②釘2箇所にカネピタ先端のリングを通し、テープを引き出します。

③テープを撓まないように張り、釘を打った遣り方貫と直交する遣り方貫にカネピタ先端にある『刻み』を当て、それを遣り方貫にマークします。

④リングを釘に掛けたまま、今度は対向する遣り方貫にもマーキングを行います。

⑤これで、それぞれの遣り方貫に仮墨①・仮墨②がマークされました。
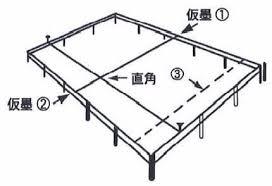
⑥仮墨①と仮墨②を結んだ線と、釘を結んだ線は直交しています。
つまり矩になっている訳です。
この線を基準にして基礎の墨を引いていけば、矩を保つことが出来るんです。
釘を結んだ線と仮墨①を結んだ三角形は、二等辺三角形になります。
だってカネピタのテープは、2枚同じ長さで出るようになっています。
金属製のテープですから、伸びたりしません。
斜辺が同じ長さであれば、二等辺三角形でしょ?
同様に仮墨②と危惧を結んだ三角形も、二等辺三角形になります。
学校の授業を思い出して下さい。
同じ長さの底辺を持つ二等辺三角形の、それぞれの頂点を結べば、その線と底辺は垂直に交わります。
こんな原理を使った工具なんですよね。
スグレモノでしょ?
実用新案らしいです。
かなり儲かっただろうなぁー。
羨ましい・・・。
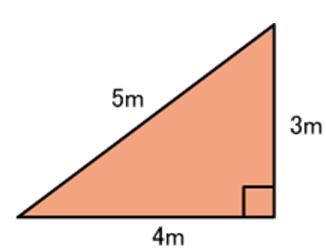
昔は、タルキを使って3:4:5の割合の三角定規をつくっていました。

こんな感じです。
これも、立派な直角三角形なんです。
だから矩を求める事が出来ます。
『大矩(オオガネ)』といいます。
遣り方貫に糸を掛け、交差した糸にこれを当てて、糸が直角になっているかどうかを見るんです。
結構いい加減な気がします。
でも、まあまあ正確なんですよね・・・。
「直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しい。」
こんな事、習いましたよね?
5の2乗は25となります。
3の2乗は9、4の2乗は16ですから、足せば25になります。
故に、この三角形は直角三角形になる訳です。
こんな所に、算数って活かされているんです。

posted by Asset Red
住所:東京都練馬区北町2-13-11
電話:03-3550-1311
東武東上線 東武練馬駅下車5分